---

1.深入淺出
 

　　上課鐘一響，這群統計學子已經就座，這個現象與上一節課的姍姍來遲成鮮明對比，他們似乎想用行動來說明他們已開始喜歡統計了。

　　為了驗証上一節的學習效果，先考考他們統計的定義是什麼？『統計就是數據透過計算產生出有意義的情報』。
 
　　異口同聲的回應，真令人飽嚐得天下英才而教之的喜悅！
　　『那麼有意義情報的構成要素是什麼呢？』
 
　『1. 集中趨勢（通常以作代表）
　　2. 離中趨勢（通常以σ作代表）
　　3. 被含蓋在特定範圍內的機率』

　　這麼正確而流暢的回答，令人一則以喜，一則以憂，喜的是他們學的實在真好，憂的是過分的熟練，會不會也是另一種形式的僵化呢？

　　於是決定幫他們在熱忱與理想之間均衡一下，使他們在熟練中仍不失應變的彈性，於是反問他們『你們的答案完全正確，但是這樣的答案對於沒有學過統計的人有沒有幫助呢？換句話說，你所計算的與σ，如何才能讓沒學過統計的人一目瞭然呢? 』

　　大家彼此對看，熱忱的臉上慢慢多了一抹沈思，學而不思則罔真是必要的提醒，有些有學問的人卻沒有影響力，根本問題也許並非懷才不遇，而是掉入了孤芳自賞的陷阱，以致於他的學問不但不能用來服務人群，反倒讓他與許多局外人壁壘分明。因此真有必要幫這群學生將思緒拉出教室，讓他們多想一想如何運用統計知識，才能幫助更多沒有學過統計的人。
 
　　思索中，有一位學生鼓起勇氣回答
 
『老師，我們可不可以把那些情報(，σ)轉換成圖形？』
『當然可以啊！但是為什麼要轉換成圖形呢？』
『因為圖形比較容易一目瞭然啊！』
 
『太好了，你這種想法與古早時統計大師構思直方圖(Frequency Histogram)時的想法正好不謀而合。』
 
然後用投影機打了一張直方圖的範例在螢幕上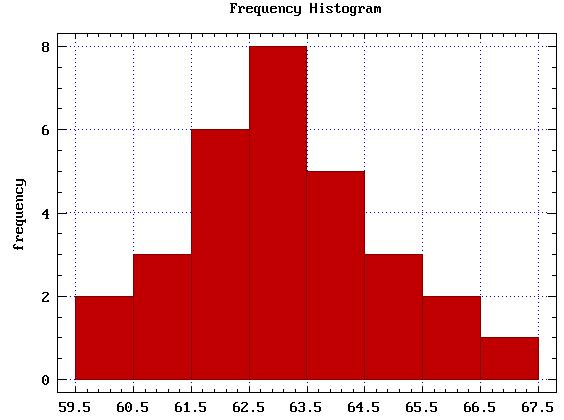
 

 圖1：直方圖

『請問對一般沒學過統計的人是與σ比較容易懂呢？還是直方圖比較容易懂呢？』


 
『直方圖！』異口同聲的回答
『對，那我們開始學直方圖好不好？』
『好！』

輕鬆學統計(2)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　張忠樸著

2.走過從前
 

　　傳統做直方圖之前要先斟酌 (1) 樣本數，然後依據樣本數來決定 (2) 分組數，然後再決定 (3) 每組之組距與組界，而後根據上述(1)(2)(3)來設計 (4)次數分配表，最後再依據次數分配表來繪製(5)直方圖
如果我們有一組數據如下：
 
63   60   64   62   63   64
63   62   66   64   60   62
61   65   62   63   66   63
67   64   63   62   65   63
65   61   62   64   63   61

那麼依據上述(1)(2)(3)(4)的步驟，我們可以得到它的次數分配表

 

組別	下組界	上組界	組中值	次數	累積次數
at  or	below	59.50		0	0
1	59.50	60.50	60.00	2	2
2	60.50	61.50	61.00	3	5
3	61.50	62.50	62.00	6	11
4	62.50	63.50	63.00	8	19
5	63.50	64.50	64.00	5	24
6	64.50	65.50	65.00	3	27
7	65.50	66.50	66.00	2	29
8	66.50	67.50	67.00	1	30
above	67.50

=63.1

σ=1.72906

根據這張次數分配表，就可以得到圖(1)的直方圖。

　　為了讓局外人明白統計量的意義，直方圖真是幫了大忙，但是相對的為了作直方圖，前輩們就必須研究分組法與下功夫作次數分配表，這都是很累人的事，所以其實不可小看深入淺出，因為它也是須要下一番功夫的。

　　所幸在電腦普及後，如今借助電腦套裝軟體，上述(1)(2)(3)(4)那些繁瑣的程序都可以用電腦來代勞，而事半功倍地獲得直方圖。
 

輕鬆學統計(2)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　張忠樸著

3.學以致用
 

　　既然我們現在可以事半功倍的獲得直方圖，那麼我們就應該將省下的時間，更多花在應用上，換句話說我們不妨要多想一想：
 
── 直方圖的目的是什麼？
── 直方圖可能有那些基本模式？
── 每一種基本模式透露了那些重要的訊息？
── 如何運用直方圖來改善品質？
『直方圖是目的嗎？』再一次用問題刺激學生去思想。

『不是！』

『那你們認為直方圖的目的該是什麼？』

『我並不確定，但是能不能與上一節課學過的常態分配圖作一些結合？』

『很好啊！但是你想怎樣結合呢？』

『我想看一下每組數據所呈現的直方圖是否與標準常態分配的形式相吻合。』

『如果吻合，那代表什麼意義呢？』

『如果吻合，那似乎証明這組數據是出自於一組近似常態分配的製程。』

　　這樣的推理邏輯真令人激賞，但是若要打通任督二脈就必須狠心將他再逼到死角。

『好極了，但是如果直方圖與常態分配不吻合呢？』
『如果不吻合..........』

他果然陷入了苦思。苦思中，他似乎又回想起上節課中反守為攻絕處逢生的那一招，靈光一閃他開始平心靜氣地反問。

輕鬆學統計(2)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　張忠樸著

4.參透玄機
 

『老師，過去的統計學家是不是已經發現了一些不吻合常態分配的基本模式？』

『沒錯，直方圖中的確有許多不吻合常態分配的案例，經過統計學家的整理，他們將這些案例歸納成三大類型，這也就成了直方圖研判的理論架構。』
 
『老師，請問用這三大『另類』直方圖來作研判時，有公信力嗎？』

這些學生真的很另類，用詞很另類，旁敲側擊的功夫更另類，明明想學三大『另類』直方圖，卻不肯明講，既然如此，那也不必明說，不妨先讓他們傷腦筋一下。

『在回答你的問題以前，請你先告訴我，在直方圖(如圖一)中的高度與寬度分別代表那些統計意義？』

『高度應該是代表集中趨勢，寬度則應該是代表離中趨勢，不知道這種想法對不對？』

『完全正確，所以正常的直方應該長什麼樣子呢？』

『應該是中間一個主峰，左右對稱下降吧！』

『沒錯，正常的直方圖理當如此，所以某一張直方圖若與正常情況明顯不同，那就表示這組數據大有玄機，現在我們來參透一下如何？』

『好啊！』

4.1來源混雜多峰並起
 

打開投影機，將下面這張直方圖投在螢幕上


 圖2A：多峰型直方圖（層別前）

等大家看過之後，請問大家

『這張直方圖有何特殊之處？』

『這張直方圖怪怪的，它有兩個主峰耶！』

『沒錯它為什麼會有兩個主峰呢？』

埋頭苦思的表情又出現了，苦思中開始自言自語.....突然，若有所悟──

『主峰代表集中趨勢，所以兩個主峰似乎是說有兩個集中趨勢混雜在同組數據之中，難道說這張直方圖.....？』

『對的，這張直方圖的原始數據的確是混合了兩個供應商的資料，所以在直方圖研判上，一般人看到多峰型就應該先用層別法來分析，至於該如何層別呢？請大家一起來想一下。』

『有時數據可能來自不同的設備，所以可以用設備來層別。』甲說，
『如果照此邏輯研判，那麼班次也可以用來層別。』乙舉一反三。
『是的，一般最常用的層別就是原料別，設備別，班次別，人員別等，以雙峰型直方圖為例，經過成功的層別後，圖二就可一分為二了。』


圖2B：多峰型直方圖（層別後）




在大家若有所悟時，進一步提醒大家──
『如果該層別的直方圖而沒有加以層別，這樣得到的及σ會有意義嗎？』
 
『沒有意義！』

『為什麼呢？』

『因為會失真，它會變成一個既不是也不是的怪物』

『好極了，但是這種未經層別的數據僅會造成失真這一種副作用嗎？』
 
一陣沈思之後，有學生舉手
 『不，除了失真外，更嚴重的後果可能反倒是會造成σ的虛胖。』

『太棒了，這個問題也正是統計學家最擔心的問題，因為統計學家早已証明虛胖後的，因此多峰型的直方圖若不先予層別就會造成的虛胖，進而造成管制界限浮濫及製程能力低估等後遺症，因此今後一看到多峰型直方圖請大家切記一定先要──』

『作層別！』異口同聲的回答。

4.2特殊原因形成離島
 
趁著他們興趣盎然，再在螢幕上投出一張直方圖
 


圖3：離島型直方圖

『請問這張直方圖有何特殊之處？』
『老師，這張直方圖右邊好像怪怪的！』

『你說怪怪的是什麼意思呢？』

『我覺得右邊偏離出去的這一小撮產品似乎大有玄機。』

『很好的觀察，所以統計學家才將這一類型的直方圖叫做離島型直方圖，顧名思義，研判的重點當然要放在離島上，換言之，這一小撮產品不會沒代沒誌的從本島游離出去，把它拉扯出去的力量可能就是統計學所謂的非機遇原因(Assignable Cause)，而遇到離島型直方圖就一定要將這些隱藏的特殊原因找出來。』
 
『請問老師，如何去找這些特殊原因呢？』
 
『在此情形下要找出真因需要運用專業技術，而非統計邏輯，這也提醒我們診斷問題的統計邏輯與解決問題的專業技術是需要相輔相成的。不過用專業技術找出的原因是否正確，倒可用統計方法來研判，那就是以後要教的統計的檢定，在下課前請大家還是回到今天的主題，請想一想，特殊型的直方圖可概分為幾種？』

『三種！』

『那麼剩下的時間讓我們來學最後一種。』

 4.3偏向一邊洞燭機先
 
『請各位先看投影片，這就是最後一型的特殊直方圖』
 


圖4：右偏型直方圖


 




『這一類的直方圖既與管理疏失所造成的數據混雜無關(詳見4.1)，又與技術原因造成的離島問題無涉(詳見4.2)。它反而可說是一種難以避免的自然現象，統計學家特別將它稱為偏態型直方圖，換言之它就是會慢慢偏向一邊，請各位想想看，在我們生活週遭，有那些類似的現象？』
 
『老師，血壓愈來愈高算不算？』真是烏鴉嘴，那壼不開提那壼。

『不算！再想想別的例子』故意給他吐糟

『老師，汽車老了就會愈來愈耗油這算不算？』

『這還差不多，其實這一類型的直方圖的確大部分都與老化有關，換言之它反映了某些品質特性的壽命曲線，例如沖模使用久了，沖出來的物件就會愈來愈粗糙，電池使用久了，能量就會逐漸衰減等等，這些現象幾乎無法避免，但是若活用偏態型直方圖卻可將損失降到最小，請各位想一想為什麼？並與大家分享你認為該如何做？』

『老師，我們可不可以先訂一個界限，一旦數據接近這個界限，我們就採取預先訂好的保養計劃，以避免問題惡化到不可收拾。』

『太好了，這個想法，正是許多公司在預防保養上實際有效的作法，讓我們給這位活用統計的同學熱烈的掌聲好嗎？』
　
　　在熱烈的掌聲中，我看到的不祗是一群喜歡追求知識的學生，我看到的更是一群熱愛將知識用來為別人服務的學生。

得英才如此，夫復何求？
 

    1 2 3                  下一页

>> 关闭窗口 <<